Sep 19

Et bîîîîîîîîîîm!

Introduction

Régulièrement, certains thèmes mathématiques font parler d’ eux. Par exemple, dans les années 90, les fractales sont revenues à la mode, probablement parce que les ordinateurs de l’ époque devenaient suffisamment puissants pour les utiliser afin de produire des images intéressantes. Il y a plus de deux siècles, Euler a étudié les sommes divergentes, et avait noté le caractère paradoxal de certaines d’ entre elles. Celle qui est devenue célèbre avec internet vers les années 2010 est la somme infinie des entiers naturels (que nous appellerons « S » dans toute la suite), à laquelle Ramanujan avait attribué la valeur -1/12. Il avait bien conscience que cela cachait un problème sous-jacent, et n’ avait pas démontré ni sa véracité ni sa fausseté de manière rigoureuse. Cet article essaie de présenter quelques arguments valables, en essayant de rester à un niveau lycée, pour déterminer à quoi pourrait être égal la somme « S ».

1 – Sommes

Ce chapitre est librement tiré de [1].

1.1 – Sommes finies

Nous ne ferons que rappeler ici quelques notations standard concernant les sommes finies.

Dans une expression du genre 1+2+3+\dots+(n-1)+n les points de suspension indiquent que l’expression doit être complétée en fonction des premiers et des derniers termes de la somme. Nous allons considérer des sommes de la forme

    \[ a_1+a_2+\dots+a_n\]

où chaque a_k est un nombre que l’ on suppose défini. L’avantage de cette notation, c’ est qu’ avec un peu d’ imagination on peut « voir » la somme comme si elle avait été écrite entièrement. Un élément a_k d’ une somme est appelé un terme. Lorsque les termes sont spécifiés par des formules, ce qui est souvent le cas, il faut faire en sorte que leur signification soit perçue sans ambiguïté. C’est pourquoi il est parfois nécessaire de les écrire sous une forme développée. Par exemple, si

    \[ 1+2+\dots+2^{n-1}\]


est supposée être une somme de n termes plutôt que de 2^{n-1} termes, il vaudrait mieux l’ écrire plus explicitement:

    \[2^0+2^1+\dots+2^{n-1}\]

Les points de suspension sont très utiles mais peuvent, d’ une part, être cause d’ambiguïté, et d’ autre part, alourdir les expressions. D’ autres notations existent, la plus utilisée étant la « notation sigma »:

    \[\label{somme}(1) \sum_{k=1}^{n}a_k\]

ainsi appelée parce qu’ elle est représentée par la lettre grecque \Sigma (sigma majuscule). Cette notation signifie qu’ il faut inclure dans la somme exactement tous les termes a_k dont l’ indice k est un entier (k \in \mathbb{N}) compris entre les deux limites 1 et n. On dit que c’ est une « somme pour k allant de 1 à n ». Le symbole \Sigma signifie que l’ on utilise l’ opération ‘+’ de la structure algébrique sous-jacente sans en changer les propriétés. Il s’ agit simplement d’ une modification cosmétique et non sémantique. Par exemple, si on étudie une somme \Sigma sur des entiers, alors l’ opération ‘+’ sous-jacente représente l’ addition sur les entiers, avec ses propriétés habituelles et bien connues. Si les éléments a_k sont des matrices, alors l’ opération ‘+’ représentera l’ addition matricielle, etc. Il s’ agit donc d’ une simple convention de notation permettant d’ améliorer la concision de l’ écriture sans en changer la signification.

La quantité écrite après \Sigma (a_k dans notre cas) s’ appelle le terme générique. La variable  d’ indice k est dite liée au signe \Sigma dans l’ équation ci-dessus, car le k de a_k est indépendant d’ éventuelles occurrences de cette même lettre k en dehors de la notation Sigma. On pourrait remplacer k par n’ importe quelle autre lettre sans changer le sens de cette somme.

Il existe aussi une notation Sigma généralisée, plus utile encore que sa forme délimitée. On écrit simplement une ou plusieurs conditions sous le \Sigma, pour spécifier l’ ensemble des indices sur lesquels on veut sommer. Par exemple, les sommes ci-dessus peuvent aussi s’ écrire

    \[\label{somme2}\sum_{1 \le k \le n}a_k\]

Dans cet exemple particulier, il n’ y a pas beaucoup de différence entre la nouvelle forme et celle de (1). Cependant la forme généralisée permet de sommer sur des ensembles d’ indices qui ne sont pas forcément des entiers consécutifs. Par exemple, on peut écrire la somme des carrés de tous les entiers positifs impairs strictement inférieurs à 100:

    \[\sum_{\substack{1 \le k < 100\\k \ {\text impair}}}k^2\]


L’ équivalent délimité de cette somme,

    \[\sum_{k=0}^{49}(2k+1)^2\]

est plus lourd et bien moins clair. De façon similaire, la somme des inverses de tous les nombres premiers entre 1 et N s’ écrit

    \[\sum_{\substack{p \le N\\p \ {\text premier}}}\frac{1}{p}.\]

Si nous voulons utiliser la forme délimitée, il faudrait écrire

    \[\sum_{k=1}^{\pi(N)}\frac{1}{p_k}\]

où p_k est le k-ième nombre premier et \pi(N) est le nombre de nombre premiers inférieurs ou égaux à N.

L’ avantage majeur de la notation Sigma généralisée est qu’ elle peut être manipulée plus aisément que la forme délimitée. Par exemple, supposons que nous voulions changer la variable d’ indice k en k+1. Si nous utilisons la forme générale, nous avons

    \[\sum_{1 \le k \le n}a_k = \sum_{1 \le k+1 \le n}a_{k+1}\]

On voit facilement ce qui se passe, et on peut faire cette substitution presque sans réfléchir. En revanche, avec la forme délimitée, on a

    \[\sum_{k=1}^{n}a_k = \sum_{k=0}^{n-1}a_{k+1}\]

Il est plus difficile de voir ce qui se passe, et donc plus facile de se tromper.

Malgré tout, la forme délimitée n’ est pas totalement inutile. Elle est esthétique, explicite, et peut s’ écrire plus vite. Nous pouvons utiliser la forme que nous souhaitons en fonction de nos besoins. Si une somme doit apparaître dans le texte d’ un paragraphe plutôt que dans une équation, nous utiliserons une version légèrement différente de (1): nous écrirons « \sum_{k=1}^{n}a_k », pour que la formule ne soit pas trop haute.

Le lecteur souhaitant se familiariser davantage avec les sommes, leurs manipulations et leurs propriétés (associativité, distributivité, commutativité) peut se reporter au chapitre 2 de [1].

1.2 – Sommes infinies

Contrairement aux sommes finies, les sommes infinies peuvent parfois conduire à des paradoxes. Elles doivent donc être définies avec beaucoup plus de rigueur afin d’ éviter de tomber sur ce type de problème. Nous verrons que ce n’ est malheureusement pas toujours possible. Mais, commençons d’ abord par les définitions habituelles utilisées pour manipuler les sommes infinies.

Considérons la somme infinie suivante

    \[Z = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + ...\]

on pourrait penser qu’ elle est égale à 2, car si on la multiplie par 2 on obtient

    \[2Z = 2 + 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ... = 2 + Z\]

Pourtant, ce même raisonnement nous conduirait à affirmer que

    \[T = 1 + 2 + 4 + 8 + 16 + 32 + ...\]

est égal à -1, car en multipliant par 2 on a

    \[2T = 2 + 4 + 8 + 16 + 32 + 64 + ... = T-1\]

Or cela est plus qu’ étrange: comment se fait-il qu’ on obtienne un nombre négatif en additionnant des quantités positives? On considère plus judicieux dans ce cas de considérer Z et T comme étant indéfinies; ou alors de dire que Z=2 et que T=\infty, ou encore de dire que ces sommes sont inconsistantes. Dans le cas de T, on lui ajoute des termes qui sont plus grands que n’ importe quel nombre fixé. Il semble qu’ il y ait une contradiction quelque part… Et s’ il y a contradiction, c’ est qu’ il y a un loup pas loin…

Reprenons au début, et voyons la définition usuelle de la valeur d’ une somme générale \sum_{k \in K}a_k, où l’ ensemble K peut être infini…

1.2.1 – Termes positifs ou nuls

Pour commencer, supposons que les termes a_k sont tous positifs ou nuls: a_k \in \mathbb{R}_{*}^{+}. Dans ce cas, voici la définition usuelle: s’il existe une constante A telle que

    \[\sum_{k \in F}a_k \le A\]

pour tout sous-ensemble fini F \subset K, alors \sum_{k \in K}a_k sera le plus petit A possible (l’ensemble de ces A a toujours un plus petit élément; cela découle de certaines propriétés bien connues des nombres réels), on dit que la somme converge vers A. Par contre, si on ne peut pas trouver une telle borne A, alors on dira que \sum_{k \in K}a_k = \infty; cela signifie que, pour tout nombre réel A, il existe un ensemble fini de termes a_k dont la somme excède A, on dit que la somme diverge vers \infty.

Dans le cas où K est l’ ensemble des entiers positifs ou nuls (ie. K = \mathbb{N}), il découle de notre définition pour les termes a_k positifs ou nuls que

    \[\sum_{k \ge 0}a_k=\lim_{n \to \infty} \sum_{k=0}^{n}a_k\]

Voici pourquoi: toute suite croissante de nombres réels a une limite (qui peut être \infty). Soit A cette limite, et soit F un ensemble quelconque d’ entiers positifs ou nuls dont tous les éléments sont \le n. On a bien sûr \sum_{k \in F}a_k \le \sum_{k=0}^{n}a_k \le A; donc, soit A=\infty soit A est un nombre qui majore \sum_{k \in F}a_k pour tout F. Soit maintenant A’ un nombre plus petit que A; alors il existe un entier n tel que \sum_{k=0}^{n}a_k > A'. Il suffit alors de prendre F = {0,1,...,n} pour voir que A’ n’est pas un majorant de \sum_{k \in F}a_k pour tout F.

Cette définition facilite grandement le calcul de certaines sommes infinies. En particulier, les sommes infinies Z et T que nous avons rencontrées ont pour valeur respectives 2 et \infty, exactement comme nous le soupçonnions.

1.2.2 – Termes négatifs et positifs

Considérons maintenant le cas d’ une somme qui peut avoir des termes négatifs aussi bien que positifs. Par exemple, quelle devrait être la valeur de la « série de Grandi » [6]:

    \[V = \sum_{k \ge 0}(-1)^k\]


En regroupant les termes par paires, on obtient

    \[V = (1-1)+(1-1)+(1-1)+\dots = 0 + 0 + 0 + \dots,\]


et ainsi de suite la somme s’annule: V=0; mais si on n’ apparie qu’ à partir du deuxième terme, on a

    \[V = 1-(1-1)-(1-1)-(1-1)-\dots = 1 - 0 - 0 - 0 - \dots\]

et la somme V vaut alors 1! En regroupant ces deux résultat, on aboutit à la contradiction que 0 = 1, ce qui, si c’ était vrai, aurait quelques répercussions sérieuses en arithmétique! On peut donc déjà se douter que notre calcul n’ est, au mieux, pas rigoureux, et au pire, faux. Il ne peut donc pas servir dans une démonstration valable! Mais, ce n’est pas fini, si nous rassemblons les termes de V de la façon suivante:

    \[V = 1 - (1-1+1-1+1-1+1- \dots)\]


en constatant que l’ intérieur de la parenthèse est V elle-même, on obtient

    \[V = 1 - V\]


ce qui donne V = \frac{1}{2}

On peut aussi essayer de poser x=-1 dans la formule \sum_{k \ge 0}x^k=1/(1-x), puisqu’ on sait qu’ elle est correcte pour 0 \le x < 1; mais alors on est forcé de conclure de nouveau que cette somme infinie V est égale à \frac{1}{2}, bien que ses termes soient tous entiers! En fait, selon la manière dont on regroupe les termes, on peut parvenir à n’ importe quel résultat, ce qui prouve que cette somme a un aspect pour le moins pathologique… Le problème vient du fait qu’ on essaie de lui attribuer une valeur, alors qu’ elle n’ a pas les caractéristiques permettant de le faire avec les méthodes classiques. Les calculs ci-dessus sont donc faux et ne peuvent donc être utilisés pour aucune démonstration valable. Ils utilisent des hypothèses habituelles sur les sommes, qui ne sont pas respectées par cette somme-ci (linéarité, stabilité, régularité, propriétés de l’ addition), on dit que cette somme est inconsistante.

Il est donc normal d’ être déconcerté de voir une somme donner des valeurs différentes selon la manière d’ additionner ses termes. Les ouvrages d’ analyse avancée proposent toute une variété de définitions permettant de donner des valeurs consistantes à des sommes inconsistantes à condition qu’ elles aient des propriétés particulières. Mentionnons la régularisation Zêta, les méthodes d’ Abel, de Cesàro, ou encore les suprêmes raffinements de la « convergence conditionnelle ». Ces méthodes imposent de changer de théorie concernant l’ addition habituelle, au profit d’ une addition généralisée qui n’ a plus les mêmes propriétés. Mentionnons que toutes ces méthodes appliquées à des sommes non pathologiques (comme Z, T et U ci-dessus), peuvent alors donner des résultats étranges mais tout à fait consistants selon ces théories alternatives, mais encore une fois, à condition que les sommes en question aient les bonnes propriétés et/ou de changer les propriétés de l’ addition utilisée. Ces méthodes dépassent largement le cadre fixé ici, mais pour les lecteurs avertis je conseille de voir l’ intégralité du lien [2].

La définition des sommes que nous utilisons ici, dite classique, permet de préserver la validité de toutes les opérations habituelles pour des sommes non pathologiques.

La définition classique des sommes infinies est très simple. Soit K un ensemble et a_k un terme à valeur réelle défini pour tout k \in K. Tout nombre réel x peut s’ écrire comme la différence de sa partie positive et sa partie négative,

    \[x=x^+-x^-, \text{ o\`u } x^+=x . [x>0] \text{ et } x^-=-x . [x<0],\]

(Il est clair que x^+=0 ou bien x^-=0). Nous savons déjà comment définir les valeurs des sommes \sum_{k \in K}a_k^+$ et $\sum_{k \in K}a_k^-, puisque les a_k^+ et les a_k^- sont positifs ou nuls. Voici donc la définition générale:

    \[\sum_{k \in K}a_k = \sum_{k \in K}a_k^+ - \sum_{k \in K}a_k^- \]

sauf si les deux sommes de droite sont égales à \infty. Dans ce dernier cas, \sum_{k \in K}a_k reste indéfinie.

Soit A^+=\sum_{k \in K}a_k^+$ et $A^-=\sum_{k \in K}a_k^-. Si A^+ et A^- sont toutes deux finies, on dit que la somme \sum_{k \in K} converge absolument vers la valeur A=A^++A^-. Si A^+=\infty et A^- est fini, on dit que la somme \sum_{k \in K} diverge vers + \infty. De façon similaire, si A^-=\infty et A^+ est finie, on dit que \sum_{k \in K} diverge vers - \infty. Si A^+=A^-=\infty, rien ne va plus, et la somme reste indéfinie, et on dira que la somme est inconsistante, et seules des méthodes alternatives évoquées ci-dessus peuvent, sous certaines conditions, lui attribuer une valeur.

Cette définition est valable on l’ a vu pour les termes positifs ou nuls, et, ainsi que nous l’ avons vu, pour tous les termes à valeur réelle. Si les termes a_k sont des nombres complexes, on peut évidemment étendre encore cette définition, mais cela ne nous intéresse pas ici.

2 – S diverge vers 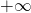+\infty

Si on utilise les notations vues au chapitre 1, la somme infinie des entiers S peut s’ écrire

    \[ S=\sum_{k \in \mathbb{N}}{a_k} \]

avec a_k=k. Donc, tout élément de cette somme est un nombre entier positif. De plus, on parle de « somme », dans notre cas, il s’ agit de l’ addition habituelle en arithmétique sur les nombres entiers. Ses propriétés font que le résultat est indépendant de l’ ordre dans lequel on additionne les entiers, et que le résultat est lui-même un nombre entier. On va voir dans ce chapitre que cette somme ne peut être « égale » (on dit « diverge vers ») qu’ à +\infty et à rien d’ autre, en particulier, pas à -\frac{1}{12} comme certaines « démonstrations » l’ affirment (voir lien [4]).

2.1 – Approche élémentaire

Compte-tenu des définitions usuelles des sommes infinies vues au paragraphe 1.2.1, nous sommes exactement dans le cas d’une somme de termes qui sont tous positifs ou nuls:

    \[S = 0 + 1 + 2 + 3 + \cdots = \sum_{k \in \mathbb{N}}a_k\]


avec a_k=k:

    \[S = \sum_{k \in \mathbb{N}}k\]


la réponse découle donc immédiatement de la définition des sommes infinies d’ entiers positifs du paragraphe 1.2.1:

    \[S = \lim_{n \to \infty} \sum_{k=0}^{n}k = +\infty\]

La somme S diverge donc vers + \infty et on ne peut lui attribuer de valeur. Il aurait fallu pour cela qu’ elle aie les bonnes propriétés (de convergence par exemple).

Poussons le bouchon, et constatons, comme vu au chapitre 1.2.2, que nous sommes dans le cas où la somme partielle \sum_{k \in K}a_k^- vaut 0 puisque notre somme ne contient aucune partie négative, il ne reste donc plus que la partie positive et on se retrouve dans le même cas que précédemment, ce qui est parfaitement cohérent:

    \[S = \sum_{k \in \mathbb{N}}k = \sum_{k \in \mathbb{N}}k^+ - \sum_{k \in \mathbb{N}}k^-\]


où

    \[\sum_{k \in \mathbb{N}}k^- = 0,\]


donc

    \[S = \sum_{k \in \mathbb{N}}k = \sum_{k \in \mathbb{N}}k^+ = \lim_{n \to \infty} \sum_{k=0}^{n}k = +\infty\]

Même conclusion donc: la somme S diverge vers + \infty et n’ a donc pas de valeur.

2.2 – Approche algébrique

Puisqu’ il s’ agit d’ une somme, sur des entiers, on peut donc se restreindre à manipuler le groupe algébrique [10] des entiers définit par <\mathbb{N}, +, 0>, où + est la loi de composition interne, commutative et associative, et 0 son élément neutre. Je re-précise bien une chose: la loi de composition + est interne. Oui, oui c’ est important, car ça signifie que si \forall a, b \in \mathbb{N}, c = a + b, alors cela implique que c \in \mathbb{N}. Mais le fait qu’ elle soit commutative est tout aussi important car cela signifie que si c = a + b, cela implique que c = b + a et réciproquement. Le fait qu’ elle soit associative, implique que quelle soit la manière de regrouper les termes, le résultat est le même: (a+b)+c=a+(b+c). A partir du moment où la loi est interne, il est donc impossible, par définition d’ aboutir à un résultat négatif pour c, voire même non entier, puisque par définition c \in \mathbb{N}, donc, impossible d’ obtenir par exemple -\frac{1}{12}.

2.3 – Approche analytique

La somme S_n des n premiers entiers, peut s’ écrire S_n=1+2+3+\dots+n. Vu qu’ il s’ agit d’ une somme finie de n termes, on peut effectuer les calculs suivants:

    \[ 2S_n = (1+2+3+\dots+(n-1)+n) \newline + (n+(n-1)\dots+3+2+1) \]

ce qui conduit à

    \[ S_n=\frac{1}{2}(1+2+3+\dots+(n-1)+n)(n+(n-1)+\dots+3+2+1) \]

soit, après simplification

    \[ S_n=\frac{n(n+1)}{2} \]

résultat que Carl Friedrich Gauss aurait démontré vers l’ age de neuf ans. Au passage, on appelle les éléments de cette somme, les nombres triangulaires [11], car ils représentent le nombre de quilles que l’ on peut mettre dans un triangle dont le nombre de lignes est n et le nombre d’ éléments par ligne est  n.

L’ avantage de cette forme close est que l’ on peut maintenant définir une fonction entière permettant d’ obtenir le résultat de la somme des x premiers entiers: \forall x \in \mathbb{N}: f(x)=S_x=\frac{x(x+1)}{2}. L’ étude de son comportement asymptotique, en utilisant le calcul des limites, fournit le résultat trivial suivant:

    \[ \lim_{x \to \infty} f(x) = + \infty \]

Ce qui là encore montre que si l’ on pousse à l’ infini le calcul de la somme des entiers, on parvient à une divergence vers l’ infini. On peut aussi encadrer la somme f par deux autres fonctions dont on sait qu’elles divergent vers + \infty, les possibilités permettant d’ aboutir à un résultat identique sont infinies…

2.4 – Approche ensembliste

On définit l’ ensemble T comme étant l’ ensemble des éléments de la somme S. On rappelle que si on peut montrer qu’ il existe une bijection entre T et \mathbb{N}, alors cela prouvera que T et \mathbb{N} ont le même nombre d’éléments et sont dénombrables. Nous allons montrer qu’ une telle bijection existe.

En fait, c’ est immédiat, puisque, comme on l’ a vu plus haut: f, définie par f(x)=\frac{x(x+1)}{2} est bien une fonction, il suffit de trouver sa réciproque f^{-1}. Après étude rapide, il me semble qu’ on peut l’ obtenir en considérant y=f(x)=\frac{x(x+1)}{2} ce qui permet d’ aboutir à 2y=x^2+x, et qui donne un magnifique trinôme du second degré bien connu x^2+x-2y=0. Il suffit alors de retenir sa racine positive:  \frac{-1+\sqrt{1+8y}}{2}}. D’où la réciproque de f: x=f^{-1}(y)=\frac{-1+\sqrt{1+8y}}{2}}.

Cette bijection entre T et \mathbb{N} permet de conclure que l’ ensemble T est dénombrable. Dit autrement, chaque élément de l’ ensemble T, soit de la somme S, possède un correspondant unique dans \mathbb{N}, et réciproquement. Comme il n’ existe pas le nombre -\frac{1}{12} dans l’ ensemble \mathbb{N} (ni d’ ailleurs aucun nombre négatif, rationnel, etc), on en déduit que ce nombre ne peut être un résultat de la somme S.

2.5 – Conclusion partielle

Nous avons parcouru différents arguments permettant de construire, si on le souhaite, une démonstration rigoureuse montrant que S ne peut que diverger vers +\infty.

3 – S converge-t’ elle vers 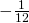-\frac{1}{12} ?

3.1 – Non

La plupart des « démonstrations » affirmant ce résultat se basent sur une astuce bien connue: elles utilisent souvent la somme indéfinie V vu au paragraphe 1.2.2, et en particulier sa valeur \frac{1}{2}, pour perturber S. Le but étant de rendre pathologique la somme S qui ne l’est pourtant pas, comme nous l’ avons expliqué.

Dans ce cas, la « démonstration » est fausse puisque V est inconsistante: nous avons en effet vu plus haut que le résultat de V dépend de la manière de regrouper les termes, autrement dit, V est indéfinie et peut donc être égal à n’ importe quelle valeur. Ce type de « démonstration », n’ a donc pas la rigueur nécessaire pour être valable et ne peux arriver à son résultat faux qu’ au terme de calculs manipulatoires que l’ on qualifie d’  »heuristiques » et qui ont donc un caractère arbitraire. Cela implique que l’ on peut aboutir à n’ importe quoi, y compris que 0=1, comme on pourrait le démontrer avec le même genre de manipulations. Lorsque ce type de paradoxe se produit, il est urgent de se demander ce qui cloche…

Certaines « démonstrations » fausses utilisent V=1/2 comme ci-dessus, mais certaines précisent « cette méthode de sommation n’ est pas permise pour des sommes infinies ».

De manière similaire le site [5] effectue le même type de raisonnement, mais devant les demandes de précisions, l’ auteur a rectifié son discours en publiant le rectificatif [4] dans lequel il précise qu’ « Affecter -1/12 à cette somme est possible sous certaines conditions » et que les « calculs heuristiques, quoique formellement faux, permettent étonnamment de retrouver cette valeur ». Tout est dit, mais cette fois avec clarté; mais on notera au passage, le paradoxe d’ un résultat considéré comme vrai à partir d’ une « démonstration » reconnue fausse…

De tout ce qui précède, avec les méthodes usuelles de sommations, et les propriétés habituelles de l’ addition, la somme S ne peut que diverger vers +\infty.

3.2 – Oui, mais non

Le plus intéressant est à venir: nous nous attachons depuis le début au fait que S=+\infty lorsqu’ on utilise les propriétés naturelles des sommes. C’ est vrai avec l’ addition habituelle. Si maintenant on décide d’ utiliser une autre méthode de sommation et/ou de changer d’ addition (ce qui revient au même), pour une autre forme d’ opération, comme l’ addition généralisée, alors on peut aboutir à d’ autres résultats. Cependant, encore une fois, ces résultats n’ ont de sens que pour des sommes ayant les bonnes propriétés, ce qui n’ est pas le cas de S.

Et le résultat le plus connu est S=-\frac{1}{12}! Et on peut l’ obtenir avec une démonstration rigoureuse autre que les calculs vus plus haut, qui n’ ont aucun sens.

Parmi ces autres méthodes de sommation, on peut citer celle de Cesaro [8] ou d’ Abel [9], mais qui ne fonctionnent pas avec S. Elle sont réservées à des sommes ayant d’ autres propriétés comme V. Une autre méthode non compatible avec notre somme S est la « régularisation par la fonction Zeta » (voir [5] par exemple) qui utilise une sommation non linéaire (ce n’ est pas le cas de S). L’ auteur exprime également l’ abandon nécessaire de la commutativité mais sans préciser pourquoi (cas d’ une somme infinie alternée de termes positifs et négatifs).

D’ autres méthodes encore, comme celle de Ramanujan [7] permettent d’ aboutir à ce même résultat. Mais toutes, imposent, une fois de plus, de laisser de côté notre bonne vieille addition classique et sa commutativité. Il ne s’ agit donc pas de notre bonne vieille somme, mais d’ un abus de langage.

Et tout comme les nombres complexes (et leur partie dite « imaginaire ») ont une utilité majeure en physique et notamment en électronique, le résultat -\frac{1}{12} est observé par exemple en mécanique quantique, où il se trouve que justement les propriétés des opérateurs quantiques ne respectent pas la commutativité…

Conclusion

Il est bien compréhensible que la plupart des vulgarisations ne puissent avoir la rigueur nécessaire à des démonstrations valables et cette page en est tout autant une victime volontaire. Une véritable démonstration mathématique exige au minimum un bon niveau de licence de mathématiques pures, ce qui est loin des prérequis fixés en introduction. D’ autre part, nous avons évoqué que pour parvenir à S=-\frac{1}{12} il est nécessaire d’ utiliser d’ autres outils que la simple addition, et qui ne sont pas forcément très accessibles, et de plus non applicables à S. La simplification est donc de rigueur dès que l’on souhaite faire partager des connaissances pointues à un public le plus large possible.

Mais simplification ne devrait pas rimer avec contre-sens (voire contre-science), par conséquent les tentatives de « démonstration » que S=-\frac{1}{12} ne prenant pas le soin d’ expliquer la nécessité de changer d’ opération peuvent être considérées comme abusives et trompeuses. En effet, des lecteurs non informés ou inattentifs pourraient se laisser berner, un peu comme on pourrait se laisser berner par une théorie complotiste devant des arguments faux mais en apparence bétonnés. Donc, si vous avez compris ou croyez avoir compris les démonstrations de ce genre de vulgarisation alors vous vous êtes peut-être faits avoir 🙂

Et pour bien comprendre d’ où vient le titre de cet article, c’ est sur le lien [3] que vous le trouverez 🙂

« Un résultat sans sa démonstration n’a aucune valeur! »

« C’ est le langage qui doit s’ adapter aux faits et non l’ inverse. Tenter d’ accommoder l’ interprétation d’ un phénomène avec un langage déjà formé et rempli d’ a-priori ne peut mener qu’ à des conclusions fausses sur la nature des choses. » –Ludwig Wittgenstein

Références

  1. Mathématiques Concrètes
  2. Science4All: hardcore 3 (à partir de 1mn et 2s)
  3. Et bîîîîîîîîm! (regardez notamment à 2mn et 56s 🙂 )
  4. 1+2+3+4+5+6+7+… = -1/12 !
  5. Le scandale des séries divergentes
  6. Série de Grandi
  7. Ramanujan’s Sommation
  8. Sommation de Cesaro
  9. Sommation d’ Abel
  10. Groupe algébrique
  11. Nombres triangulaires
  12. La somme des entiers positifs fait-elle vraiment -1/12?
  13. Numberphile v. Math: the truth about 1+2+3+…=-1/12

  14. Devenir riche grâce aux maths (la fonction Zeta de Riemman)

 

 

 

nick

Laisser un commentaire

Votre adresse de messagerie ne sera pas publiée.