Introduction
Parmi les innombrables curiosités mathématiques, je souhaite parler ici de la notion d’ infini. Sans-doute avez vous déjà entendu parler d’ ensembles infinis, et peut-être même avez-vous déjà entendu l’ expression « rien n’ est plus grand que l’ infini ». Et bien c’ est faux: il existe des infinis plus grands que d’ autres! Il existe même une infinité d’ infinis de tailles différentes! C’ est ce que je voudrais tenter de présenter ici, ainsi qu’ une conséquence dans le domaine de l’ informatique, et ce, de manière accessible. Mais rappelons d’ abord quelques notions et un minimum de formalisme après avoir vu quelques paradoxes sur les ensembles et l’ infini.
Quelques paradoxes sur les ensembles
1. L’antinomie de B. Russell
B. Russell classe les ensembles en deux sortes: ceux qui ne se contiennent pas eux-même comme élément et ceux qui se contiennent eux-mêmes. On dit qu’un ensemble est « normal » si, et seulement si, il ne se contient pas lui-même comme élément. Il est dit « non normal » dans le cas contraire.
- Exemple d’ensemble normal: l’ensemble des mathématiciens, car cet ensemble n’est évidemment pas lui-même un mathématicien.
- Exemple d’ensemble non normal: l’ensemble de toutes les choses pensables. Cet ensemble est lui-même une chose pensable, donc un élément de lui-même.
Appelons N l’ensemble de tous les ensembles normaux. La question est de savoir si N lui-même est un ensemble normal. Si N est normal, c’est un élément de lui-même (puisque, par définition, N contient tous les ensembles normaux); mais, dans ce cas, N est non normal, puisque, par définition, un ensemble qui se contient lui-même comme élément est non normal. D’un autre coté, si N est non normal, c’est un élément de lui-même (par définition du non normal), mais, dans ce cas, N est normal, puisque par définition, les éléments de N sont les ensembles normaux. Cela conduit donc à la contradiction que « N est normal » est à la fois vrai et faux.
2. L’ urne aux boules
On a d’ un coté, une urne infiniment grande et d’ un autre, un nombre infini de boules numérotées de 1 en 1 à partir de 1. A chaque étape numéro n, on effectue les 2 opérations suivantes consécutivement: on prend les boules de n à n+9 qu’ on place dans l’ urne, puis on enlève de l’ urne la boule numéro n. A la première étape, il y a donc dans l’ urne les boules de 2 à 10. A la seconde étape, il y a les boules 3 à 20, etc. La question est de savoir combien de boules contient l’ urne après un nombre infini d’ étapes. La démonstration formelle conduit à la conclusion que l’ urne est vide, ce qui est paradoxal, puisqu’ à chaque étape on met 10 boules et on en enlève une, ce qui revient à mettre 9 boules…
3. L’ hôtel de Hilbert
C’ est sans doute l’ un des paradoxes les plus connus sur les ensembles. Je me contente donc de le citer, mais voici un lien qui en parle très bien: https://fr.wikipedia.org/wiki/H%C3%B4tel_de_Hilbert.
Ensembles
Nombre de paradoxes proviennent de définitions imprécises ou pas assez rigoureuses. Ces paradoxes et les questions qui en découlent, ont historiquement une part de responsabilité de la nécessité de mettre au point une véritable théorie axiomatique des ensembles, vraiment rigoureuse. Ce n’est pas l’objectif de cet article, néanmoins, nous aurons besoin de quelques définitions.
De manière simple, un ensemble est un tas de trucs. Par exemple, l’ ensemble des lettres de l’ alphabet, l’ ensemble des mots du dictionnaire, l’ ensemble des brins d’ herbe de votre jardin, l’ ensemble des parties d’ échec possibles, etc. Les trucs contenus dans un ensemble portent le nom d’ éléments. Pour indiquer qu’ un élément ![]() appartient à un ensemble
appartient à un ensemble ![]() , on écrit
, on écrit ![]() , inversement, lorsqu’ un élément
, inversement, lorsqu’ un élément ![]() n’ appartient pas à un ensemble
n’ appartient pas à un ensemble ![]() , on l’ écrit
, on l’ écrit ![]() . Le nombre d’ éléments contenu dans un ensemble
. Le nombre d’ éléments contenu dans un ensemble ![]() s’ appelle le cardinal de l’ ensemble et se note
s’ appelle le cardinal de l’ ensemble et se note ![]() . Ce nombre peut être un entier positif dans le cas d’ un ensemble contenant un nombre fini d’ éléments (ensemble fini), ou infini dans le cas d’ un ensemble contenant un nombre infini d’ éléments (ensemble infini). Un sous-ensemble
. Ce nombre peut être un entier positif dans le cas d’ un ensemble contenant un nombre fini d’ éléments (ensemble fini), ou infini dans le cas d’ un ensemble contenant un nombre infini d’ éléments (ensemble infini). Un sous-ensemble ![]() d’ un ensemble
d’ un ensemble ![]() désigne simplement une partie de
désigne simplement une partie de ![]() , on note
, on note ![]() , qui se lit: «
, qui se lit: « ![]() est inclus dans
est inclus dans ![]() « .
« .
Exemple: considérons l’ ensemble de toutes les données que l’ on peut stocker sur un CD Audio. Les données stockées sur un CD ne sont qu’ une suite de bits (chiffres binaires valant 0 ou 1), c’ est-à-dire un nombre binaire. Si on considère un CD de 700 Mo, celui-ci permet de stocker un total de 700 * 1024 * 1024 * 8 bits (soit 5 872 025 600 bits). Chaque bit ne pouvant avoir que 2 valeurs possibles, le cardinal de l’ ensemble de tous les CD différents possibles vaut donc ![]() , ce qui est un nombre entier certes grand, mais fini. Même raisonnement pour un DVD, Blu-ray, ou tout autre support de stockage binaire et fini, seules les quantités changent.
, ce qui est un nombre entier certes grand, mais fini. Même raisonnement pour un DVD, Blu-ray, ou tout autre support de stockage binaire et fini, seules les quantités changent.
Certains ensembles étant très utilisés, il portent un nom qui permet de les identifier sans ambiguïté. Voici les noms des principaux ensembles infinis rencontrés jusqu’ au lycée:
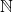 : l’ ensemble des nombres naturels (ce sont les entiers positifs) regroupe les nombres entiers à partir de 0: 0, 1, 2, 3, …, jusqu’ à l’ infini
: l’ ensemble des nombres naturels (ce sont les entiers positifs) regroupe les nombres entiers à partir de 0: 0, 1, 2, 3, …, jusqu’ à l’ infini 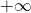 .
.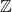 : l’ ensemble des entiers relatifs regroupe les nombres de
: l’ ensemble des entiers relatifs regroupe les nombres de  à 0 et de 0 à
à 0 et de 0 à 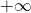 : il est constitué, en quelque sorte, de 2 ensembles
: il est constitué, en quelque sorte, de 2 ensembles 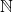 dont l’ un contient un moins devant tous ses éléments, « soudés ensembles » sur l’ élément 0.
dont l’ un contient un moins devant tous ses éléments, « soudés ensembles » sur l’ élément 0. : l’ ensemble des nombres rationnels regroupe les nombres que l’ on peut écrire sous la forme d’ un quotient entre 2 nombres relatifs:
: l’ ensemble des nombres rationnels regroupe les nombres que l’ on peut écrire sous la forme d’ un quotient entre 2 nombres relatifs: 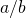 avec
avec  et
et 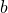 éléments de
éléments de 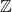 .
.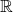 : l’ ensemble des nombres réels qui regroupe les nombres décimaux (nombres comme ceux de
: l’ ensemble des nombres réels qui regroupe les nombres décimaux (nombres comme ceux de 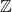 mais avec en plus une partie après la virgule).
mais avec en plus une partie après la virgule).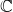 : l’ ensemble des nombres complexes regroupe l’ infinité des nombres qui s’ écrivent sous la forme de la somme de deux nombres réels, dont l’ un se nomme partie réelle, et l’ autre, partie imaginaire, elle-même précédée de la lettre i:
: l’ ensemble des nombres complexes regroupe l’ infinité des nombres qui s’ écrivent sous la forme de la somme de deux nombres réels, dont l’ un se nomme partie réelle, et l’ autre, partie imaginaire, elle-même précédée de la lettre i: 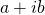 avec
avec  et
et 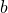 éléments de
éléments de 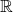 .
.
Un fait important est que tous ces ensembles forment une hiérarchie dans le sens où les plus hauts dans la liste constituent une partie des suivants, c’ est-à-dire que l’ on a ![]() . Autrement dit, tous les éléments de
. Autrement dit, tous les éléments de ![]() sont aussi dans
sont aussi dans ![]() , dont tous les éléments sont aussi dans
, dont tous les éléments sont aussi dans ![]() , etc. Comme ce sont tous des ensembles infinis on voit que se profile la notion de taille: comment par exemple
, etc. Comme ce sont tous des ensembles infinis on voit que se profile la notion de taille: comment par exemple ![]() pourrait contenir
pourrait contenir ![]() de chaque coté de zéro sans être deux fois plus grand que lui?
de chaque coté de zéro sans être deux fois plus grand que lui?
Bijections
De manière informelle, une bijection entre 2 ensembles est une relation particulière entre les éléments de ces deux ensembles: tous les éléments de l’ un sont en correspondance avec tous les éléments de l’ autre, de sorte qu’ aucun élément ne se trouve sans correspondant et qu’ aucun élément n’ aie plus d’ un correspondant. On voit bien que si une bijection existe entre deux ensembles, c’ est que ceux-ci doivent avoir le même nombre d’ éléments.
Une bijection peut porter un nom et s’ exprimer simplement par une phrase ou par une expression mathématique qu’ on appelle une fonction. Par exemple une bijection ![]() entre deux ensembles
entre deux ensembles ![]() et
et ![]() fait correspondre à tout élément
fait correspondre à tout élément ![]() de l’ ensemble
de l’ ensemble ![]() , son image
, son image ![]() dans
dans ![]() , que l’on appelle alors
, que l’on appelle alors ![]() et qui se calcule. La bijection inverse existe forcément et se note
et qui se calcule. La bijection inverse existe forcément et se note ![]() : à partir de
: à partir de ![]() un élément de
un élément de ![]() on obtient
on obtient ![]() , son correspondant dans
, son correspondant dans ![]() :
: ![]() .
.
Exemple: considérons la bijection ![]() , qui à chaque élément
, qui à chaque élément ![]() de
de ![]() lui ajoute 1 pour obtenir son correspondant dans
lui ajoute 1 pour obtenir son correspondant dans ![]() : on aura
: on aura ![]() (pour tout
(pour tout ![]() ). Réciproquement, à partir de tout élément
). Réciproquement, à partir de tout élément ![]() de
de ![]() , pour obtenir son correspondant dans
, pour obtenir son correspondant dans ![]() , il faut lui ôter 1:
, il faut lui ôter 1: ![]() (pour tout
(pour tout ![]() ).
).
Qu’ est-ce-qu’ un ensemble dénombrable?
Les infinis ont longtemps posé problème en mathématiques avant que G. Cantor ne s’ y intéresse. En 1874, il pose les premières briques de la théorie des ensembles. Cette théorie définit notamment, de manière rigoureuse, les notions d’ ensembles et d’ infinis. Elle permet, entre autre, de résoudre de nombreux paradoxes dont ces notions étaient à l’ origine, en partie à cause de leur imprécision. Elle introduit notamment la définition suivante afin de pouvoir comparer le nombre d’ éléments entre deux ensembles.
Un ensemble est dénombrable s’ il peut être mis en bijection avec ![]() . Une façon simple de le dire est qu’ un ensemble est dénombrable si on peut numéroter ses éléments, ou encore, si on peut coder avec un nombre entier unique chacun de ses éléments.
. Une façon simple de le dire est qu’ un ensemble est dénombrable si on peut numéroter ses éléments, ou encore, si on peut coder avec un nombre entier unique chacun de ses éléments.
On note ![]() le cardinal de l’ ensemble
le cardinal de l’ ensemble ![]() , il correspond au premier niveau d’ infini, l’ infini dénombrable (G. Cantor était de culture juive, ce qui explique ce choix de la première lettre de l’ alphabet hébraïque
, il correspond au premier niveau d’ infini, l’ infini dénombrable (G. Cantor était de culture juive, ce qui explique ce choix de la première lettre de l’ alphabet hébraïque ![]() « aleph »).
« aleph »).
Une conséquence de tout ce que nous avons vu jusqu’ ici est que deux ensembles ![]() et
et ![]() dénombrables vérifient
dénombrables vérifient ![]() , ils ont donc le même nombre infini d’éléments.
, ils ont donc le même nombre infini d’éléments.
Exemples d’ ensembles dénombrables
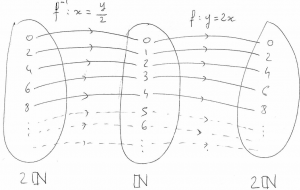
1. L’ ensemble des nombres pairs
L’ ensemble ![]() des nombres pairs est dénombrable. On pourrait penser à tort que
des nombres pairs est dénombrable. On pourrait penser à tort que ![]() est deux fois plus petit que
est deux fois plus petit que ![]() , et bien il n’ en est rien! En effet, il suffit de considérer la bijection
, et bien il n’ en est rien! En effet, il suffit de considérer la bijection ![]() qui consiste à multiplier par 2 chaque élément de
qui consiste à multiplier par 2 chaque élément de ![]() pour tomber sur son correspondant pair dans
pour tomber sur son correspondant pair dans ![]() :
: ![]() . Réciproquement, il suffit de diviser par 2 n’importe quel élément de
. Réciproquement, il suffit de diviser par 2 n’importe quel élément de ![]() pour tomber sur son correspondant dans
pour tomber sur son correspondant dans ![]() :
: ![]() . On a bien le même nombre infini d’éléments entre les ensembles
. On a bien le même nombre infini d’éléments entre les ensembles ![]() et
et ![]() , qui ont donc la même taille:
, qui ont donc la même taille: ![]() .
.
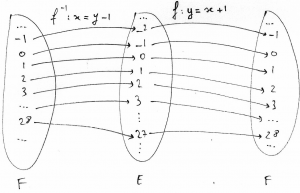
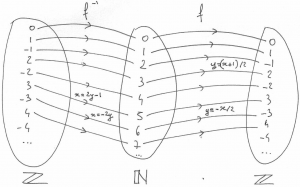
2. L’ ensemble des nombres entiers relatifs
L’ ensemble ![]() des entiers relatifs est dénombrable. Là aussi, on pourrait se fier aux apparences et donc croire qu’ il est deux fois plus grand que
des entiers relatifs est dénombrable. Là aussi, on pourrait se fier aux apparences et donc croire qu’ il est deux fois plus grand que ![]() , mais c’ est faux! Pour s’ en convaincre, il suffit de considérer la bijection qui associe les nombres de
, mais c’ est faux! Pour s’ en convaincre, il suffit de considérer la bijection qui associe les nombres de ![]() à ceux de
à ceux de ![]() ainsi:
ainsi: ![]() . Pour caractériser cette bijection, en notant
. Pour caractériser cette bijection, en notant ![]() élement de
élement de ![]() et
et ![]() élément de
élément de ![]() , on distingue 2 cas:
, on distingue 2 cas:
- si
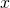 est pair, on obtient
est pair, on obtient 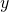 par
par 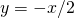
- si
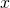 est impair, on obtient
est impair, on obtient 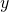 par
par 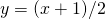 .
.
Pour la réciproque:
- si
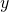 est positif, on obtient
est positif, on obtient 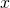 par
par 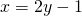
- si
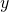 est négatif ou nul, on obtient
est négatif ou nul, on obtient 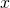 par
par 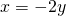 .
.
Ici encore les ensembles ont donc le même cardinal: ![]() .
.
3. Langage engendré par un alphabet
Soit ![]() un alphabet fini (un ensemble fini d’ éléments qu’ on nomme des lettres). L’ ensemble de tous les mots (un mot est une suite finie de lettres) formables avec cet alphabet (que l’ on note
un alphabet fini (un ensemble fini d’ éléments qu’ on nomme des lettres). L’ ensemble de tous les mots (un mot est une suite finie de lettres) formables avec cet alphabet (que l’ on note ![]() et que l’ on appelle langage engendré par
et que l’ on appelle langage engendré par ![]() , ou encore
, ou encore ![]() ) est dénombrable. Il suffit de numéroter les mots, par exemple, ainsi:
) est dénombrable. Il suffit de numéroter les mots, par exemple, ainsi: ![]() . Avec
. Avec ![]() représentant le mot vide. Comme notre méthode de numérotation n’ oublie aucun mot possible, il s’ agit bien d’ une bijection. Donc l’ ensemble de tous les mots formables avec l’ alphabet
représentant le mot vide. Comme notre méthode de numérotation n’ oublie aucun mot possible, il s’ agit bien d’ une bijection. Donc l’ ensemble de tous les mots formables avec l’ alphabet ![]() est dénombrable. Grâce à un théorème, ce résultat se généralise à tout alphabet fini. Donc, tout langage
est dénombrable. Grâce à un théorème, ce résultat se généralise à tout alphabet fini. Donc, tout langage ![]() engendré par un alphabet fini
engendré par un alphabet fini ![]() est dénombrable, il s’ agit d’ un résultat fondamental en théorie des langages (présenté ici sans démonstration).
est dénombrable, il s’ agit d’ un résultat fondamental en théorie des langages (présenté ici sans démonstration).
4. L’ ensemble des programmes informatiques
L’ ensemble ![]() des programmes exécutable par une machine binaire, comme un ordinateur, est dénombrable. C’ est exactement le même cas que ci-dessus avec
des programmes exécutable par une machine binaire, comme un ordinateur, est dénombrable. C’ est exactement le même cas que ci-dessus avec ![]() , et le fait que
, et le fait que ![]() (l’ ensemble de tous les programmes binaires n’ est qu’ un sous-ensemble de tous les mots possiblement formables avec
(l’ ensemble de tous les programmes binaires n’ est qu’ un sous-ensemble de tous les mots possiblement formables avec ![]() ). En effet, tous les mots engendrés par
). En effet, tous les mots engendrés par ![]() ne sont pas des programmes valides. Ce résultat (présenté sans démonstration ici) se généralise à tout langage de programmation et à tout système de calcul formel, mais cela dépasse largement le cadre fixé ici (cf. l’ isomorphisme de Curry Howard ainsi que la Thèse de Church).
ne sont pas des programmes valides. Ce résultat (présenté sans démonstration ici) se généralise à tout langage de programmation et à tout système de calcul formel, mais cela dépasse largement le cadre fixé ici (cf. l’ isomorphisme de Curry Howard ainsi que la Thèse de Church).
Qu’ est-ce-qu’ un ensemble non-dénombrable?
Un ensemble ![]() est non dénombrable (ou indénombrable) s’ il n’ existe aucune bijection entre
est non dénombrable (ou indénombrable) s’ il n’ existe aucune bijection entre ![]() et
et ![]() . Pour montrer qu’ un ensemble est non dénombrable, G. Cantor a introduit l’ argument de la diagonalisation permettant d’ élaborer une preuve, souvent par l’ absurde (on l’ appelle souvent la diagonale de Cantor). C’ est ainsi qu’ il démontra que l’ ensemble
. Pour montrer qu’ un ensemble est non dénombrable, G. Cantor a introduit l’ argument de la diagonalisation permettant d’ élaborer une preuve, souvent par l’ absurde (on l’ appelle souvent la diagonale de Cantor). C’ est ainsi qu’ il démontra que l’ ensemble ![]() des nombres réels est non-dénombrable (cf. la démonstration sur wikipedia que je reprend ci-dessous de manière informelle).
des nombres réels est non-dénombrable (cf. la démonstration sur wikipedia que je reprend ci-dessous de manière informelle).
On considère le sous-ensemble ![]() de
de ![]() (les nombres compris entre 0 et 1 exclus) à partir duquel on va construire un nombre qui n’ appartient pas à
(les nombres compris entre 0 et 1 exclus) à partir duquel on va construire un nombre qui n’ appartient pas à ![]() . Les éléments de
. Les éléments de ![]() sont donc des nombres décimaux dont la partie entière vaut 0 et la partie décimale peut contenir un nombre infini de chiffres. On construit un tableau T contenant en ligne chaque partie décimale des éléments de
sont donc des nombres décimaux dont la partie entière vaut 0 et la partie décimale peut contenir un nombre infini de chiffres. On construit un tableau T contenant en ligne chaque partie décimale des éléments de ![]() et en colonne les chiffres de cette partie décimale. Ainsi, T(n, m) désigne la m-ième décimale du nombre se trouvant en ligne n. Chaque élément de
et en colonne les chiffres de cette partie décimale. Ainsi, T(n, m) désigne la m-ième décimale du nombre se trouvant en ligne n. Chaque élément de ![]() , par exemple 0, 4895397 se trouve quelque part dans le tableau T, disons en ligne k, ainsi T(k, 1) vaut 4, T(k, 2) vaut 8, T(k, 3) vaut 9, etc.:
, par exemple 0, 4895397 se trouve quelque part dans le tableau T, disons en ligne k, ainsi T(k, 1) vaut 4, T(k, 2) vaut 8, T(k, 3) vaut 9, etc.:
| T | 1 | 2 | 3 | 4 | 5 | … | m | … |
| 1 | ||||||||
| 2 | ||||||||
| … | ||||||||
| k | 4 | 8 | 9 | 5 | 3 | 9 | 7 | … |
| … | ||||||||
| n | ||||||||
| … |
Maintenant, on va considérer le nombre x=0,… construit en respectant la règle suivante: si T(n, n) vaut 0, alors la n-ième décimale de x vaut 1, si T(n, n) est différent de 0, alors la n-ième décimale de x vaut 2.
Notre nombre x appartient bien à ![]() , puisqu’ il est compris entre 0 et 1. Mais il n’ est dans aucune ligne du tableau, car sa partie décimale n’ est présente sur aucune ligne: il ne peut être en ligne 1 puisque la première décimale de T(1,1) est différente de la première décimale de x, même chose pour la ligne 2, T(2,2) est différente de la seconde décimale de x, etc. Donc x n’ est pas dans le tableau, donc le tableau ne contient pas tous les éléments de
, puisqu’ il est compris entre 0 et 1. Mais il n’ est dans aucune ligne du tableau, car sa partie décimale n’ est présente sur aucune ligne: il ne peut être en ligne 1 puisque la première décimale de T(1,1) est différente de la première décimale de x, même chose pour la ligne 2, T(2,2) est différente de la seconde décimale de x, etc. Donc x n’ est pas dans le tableau, donc le tableau ne contient pas tous les éléments de ![]() , donc
, donc ![]() est suffisamment grand pour n’ être pas dénombrable, ce qui implique que
est suffisamment grand pour n’ être pas dénombrable, ce qui implique que ![]() non plus, puisqu’ il contient
non plus, puisqu’ il contient ![]() .
.
Conclusion: le cardinal de ![]() est très supérieur à celui de
est très supérieur à celui de ![]() . Ce nouvel infini, de second niveau est donc plus grand que
. Ce nouvel infini, de second niveau est donc plus grand que ![]() , on le nomme l’ infini indénombrable (ou infini continu) et on note son cardinal
, on le nomme l’ infini indénombrable (ou infini continu) et on note son cardinal ![]() . On dit que le cardinal de l’ ensemble
. On dit que le cardinal de l’ ensemble ![]() a la puissance du continu, et un résultat étonnant est que
a la puissance du continu, et un résultat étonnant est que ![]() (cf. ci-dessous pour l’ explication).
(cf. ci-dessous pour l’ explication).
Exemples d’ ensembles non-dénombrables
1. L’ ensemble de toutes les fonctions entières à un seul argument entier
Une fonction entière est une fonction qui donne un nombre entier à partir de ses arguments. Par exemple la fonction addition qui prend 2 arguments entiers x et y et qui donne leur somme, elle aussi, un nombre entier: addition(x, y) = x+y. La fonction addition possède deux arguments: les deux nombres entiers x et y, mais ici, on ne parle que des fonctions à un unique argument entier et qui retournent un nombre entier.
L’ ensemble ![]() de toutes les fonctions à un seul argument entier est non dénombrable et l’ argument de la diagonalisation nous permet de voir pourquoi. Pour cela, imaginons la construction du tableau T d’ un nombre infini de lignes et de colonnes, avec en colonne les arguments entiers de 0 à
de toutes les fonctions à un seul argument entier est non dénombrable et l’ argument de la diagonalisation nous permet de voir pourquoi. Pour cela, imaginons la construction du tableau T d’ un nombre infini de lignes et de colonnes, avec en colonne les arguments entiers de 0 à ![]() et en lignes les éléments de l’ ensemble
et en lignes les éléments de l’ ensemble ![]() qui sont donc des fonctions à un seul argument entier que l’ on numérote en séquence:
qui sont donc des fonctions à un seul argument entier que l’ on numérote en séquence:
| 0 | 1 | 2 | … | … | ||
| … | … | |||||
| … | … | |||||
| … | … | … | … | … | … | … |
| … | … | |||||
| … | … | … | … | … | … | … |
Toutes les fonctions à un seul entier sont donc par construction dans ce tableau T. Par exemple, la case T(n, m) du tableau représente la fonction ![]() appliquée à l’ entier
appliquée à l’ entier ![]() . Cette case possède une valeur entière qui ne nous intéresse pas, et qu’ on ne peut de toute façon pas déterminer. Maintenant, on va considérer une nouvelle fonction, toujours à un seul argument entier, que l’ on va appeler G et que l’ on va définir ainsi: G(x) = T(x, x)+1. La question est: où se trouve G dans notre tableau? La réponse est: nulle part… Cette fonction n’ appartenant pas au tableau sensé contenir toutes les fonctions à un seul argument entier, on en déduit que le tableau ne les contient pas toutes, donc l’ ensemble
. Cette case possède une valeur entière qui ne nous intéresse pas, et qu’ on ne peut de toute façon pas déterminer. Maintenant, on va considérer une nouvelle fonction, toujours à un seul argument entier, que l’ on va appeler G et que l’ on va définir ainsi: G(x) = T(x, x)+1. La question est: où se trouve G dans notre tableau? La réponse est: nulle part… Cette fonction n’ appartenant pas au tableau sensé contenir toutes les fonctions à un seul argument entier, on en déduit que le tableau ne les contient pas toutes, donc l’ ensemble ![]() est non dénombrable et a donc la taille de l’ infini continu.
est non dénombrable et a donc la taille de l’ infini continu.
2. L’ ensemble des fonctions entières à plus d’ un argument entier
Le résultat précédent se généralise à l’ ensemble des fonctions entières à 2 arguments entiers, à 3 arguments entiers, et même à une infinité dénombrable d’ arguments entiers. La démonstration, hors propos ici, tient au fait que l’ on peut ‘coder’ par un unique entier la liste des arguments entiers (un peu comme pour un alphabet comme vu ci-dessus). Donc l’ ensemble de toutes les fonctions entières est non-dénombrable et a la taille de l’ infini continu.
3. L’ ensemble des parties d’ un ensemble
Derrière ce nom barbare se cache l’ ensemble de toutes les combinaisons de sous-ensembles que l’ on peut former à partir d’ un ensemble ![]() , on le note généralement
, on le note généralement ![]() .
.
Si ![]() est fini, alors
est fini, alors ![]() est fini et contient
est fini et contient ![]() éléments (issu d’ un théorème dont la démonstration est hors de propos ici).
éléments (issu d’ un théorème dont la démonstration est hors de propos ici).
Par exemple, avec l’ ensemble ![]() , on peut former
, on peut former ![]() parties:
parties:
- l’ ensemble vide: {} (que l’ on note aussi
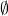 ).
). - l’ ensemble ne contenant que a: {a}
- l’ ensemble ne contenant que b: {b}
- l’ ensemble ne contenant que c: {c}
- l’ ensemble contenant a et b: {a, b}
- l’ ensemble contenant b et c: {b, c}
- l’ ensemble contenant a et c: {a, c}
- l’ ensemble contenant a, b et c: {a, b, c}
Si ![]() est infini dénombrable, alors le nombre de ses parties est égal à
est infini dénombrable, alors le nombre de ses parties est égal à ![]() , mais en revanche,
, mais en revanche, ![]() n’ est pas dénombrable. Ce résultat fondamental en théorie de ensembles est issu du théorème de Cantor, qui utilise là-encore l’ argument de la diagonalisation. On retrouve le résultat présenté ci-dessus, mais cette fois-ci, on comprend bien d’ où sort l’ égalité
n’ est pas dénombrable. Ce résultat fondamental en théorie de ensembles est issu du théorème de Cantor, qui utilise là-encore l’ argument de la diagonalisation. On retrouve le résultat présenté ci-dessus, mais cette fois-ci, on comprend bien d’ où sort l’ égalité ![]() .
.
4. L’ ensemble des fonctions réelles à un seul argument réél
On a déjà vu ci-dessus que ![]() et que
et que ![]() . Du coup, en voulant appliquer la même méthode qu’ au point 1 plus haut, on se heurterait au fait que le tableau T ne peut être construit puisque le nombre de colonnes est infini continu…
. Du coup, en voulant appliquer la même méthode qu’ au point 1 plus haut, on se heurterait au fait que le tableau T ne peut être construit puisque le nombre de colonnes est infini continu…
Et au-delà, la diagonale du fou?
Nous n’ irons guère plus loin ici, mais G. Cantor a démontré qu’ il existe des infinis encore plus grand que les deux que nous avons présenté ici. Il a même découvert qu’ il existe une infinité d’ infinis de cardinalités différentes. Ce résultat fondamental en théorie des ensembles est connu sous le nom de théorème de Cantor.
Il se serait également interrogé sur l’ existence ou non d’ infinis de tailles intermédiaire. Par exemple:
- existe-t’ il un infini de cardinalité située entre
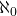 et
et 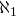 ?
? - est-ce-que le passage de
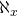 à
à 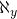 est continu ou bien se fait-il de manière discrète, c’est-à-dire par saut?
est continu ou bien se fait-il de manière discrète, c’est-à-dire par saut? - dans le dernier cas, de quelles valeurs sont les sauts?
Sa quête de réponses à ces questions l’ aurait, parait-il, sérieusement perturbé, voire rendu fou…
Une conséquence concrète
Quelque soit le langage de programmation choisi, basé sur un alphabet fini de symboles, l’ ensemble de tous les programmes que l’ on peut écrire avec ce langage est dénombrable. Donc l’ ensemble de tous les programmes informatiques pouvant être écrit avec n’ importe quel langage élaboré avec un alphabet fini est dénombrable.
De manière très simpliste, un programme informatique ne fait qu’ exécuter une ou un très grand nombre de fonctions mathématiques. Or, on a vu plus haut que l’ ensemble des fonctions n’ est pas dénombrable: il est de taille incommensurablement plus grande que celui des programmes.
Conclusion: il existe des fonctions qui ne peuvent être calculées par aucun programme informatique. Il existe donc des problèmes, qui une fois mis sous forme de fonctions mathématiques, ne pourront jamais être solubles par aucun programme informatique. Ce résultat est fondamental, et n’ a rien à voir avec une puissance de machine et/ou de langage de programmation: il pose les limites de l’ informatique et plus généralement de tout système de calcul formel, il est à la base de la théorie de la calculabilité (hors sujet ici).
Pour en savoir plus
Quelques liens sur wikipedia:
- G. Cantor
- L’ antinomie de Russell
- Ensembles dénombrables
- Ensembles non dénombrables
- Cardinalité d’ un ensemble
- L’ hypothèse du continu
- L’ ensemble des parties d’ un ensemble
- Le théorème de Cantor